下面的定义与图,都适合任何周期的 K 线图。先看下图,图中的小线段代表的是 K线,这里不分阳线阴线,只看 K 线的高低点。
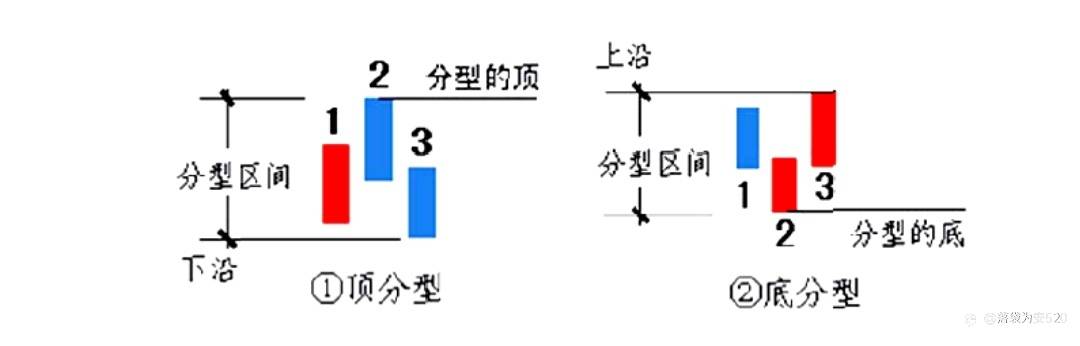
如图 1 所示,第二 K 线高点是相邻三 K 线高点中最高的,而低点也是相邻三 K 线低点中最高的,本理论给一个定义叫顶分型;如图 2 所示,第二 K 线低点是相邻三 K 线低点中最低的,而高点也是相邻三 K 线高点中最低的,本理论给一个定义叫底分型。看不明白定义的看图就明白了,图形更直观。
顶分型的最高点叫该分型的顶,底分型的最低点叫该分型的底,由于顶分型的底和底分型的顶是没有意义的,所以顶分型的顶和底分型的底就可以简称为顶和低。也就是说,当我们以后说顶和底时,就分别是说顶分型的顶和底分型的底。在实际图形里,对于分型,最大的麻烦就是前后K线间的包含关系,如图3所示,所谓的包含关系就是一K线的高低点全在另一K线的范围里。

这种情况下,可以这样处理,在向上时,把两K线的最高点当高点,而两K线低点中的较高者当成低点,这样就把两K线合并成一新的K线;反之当向下时,把两K线的最低点当低点,而两K线高点中的较低者当成高点,这样就把两K线合并成一新的K线。经过这样的处理,所有K线图都可以处理成没有包含关系的图形。
上面说向上、向下,那什么是向上?什么是向下?其实这根本没什么可说的,任何看过图的都知道什么是向上,什么是向下。
假设第n根K线满足第n根与第n 1根的包含关系,而第n根与第n-1根不是包含关系,那么,如果gn>=gn-1,那么就称第 n-1、n、n 1根K线是向上的;如果 dn<=dn-1,那么就称第n-1、n、n 1根K线是向下的。

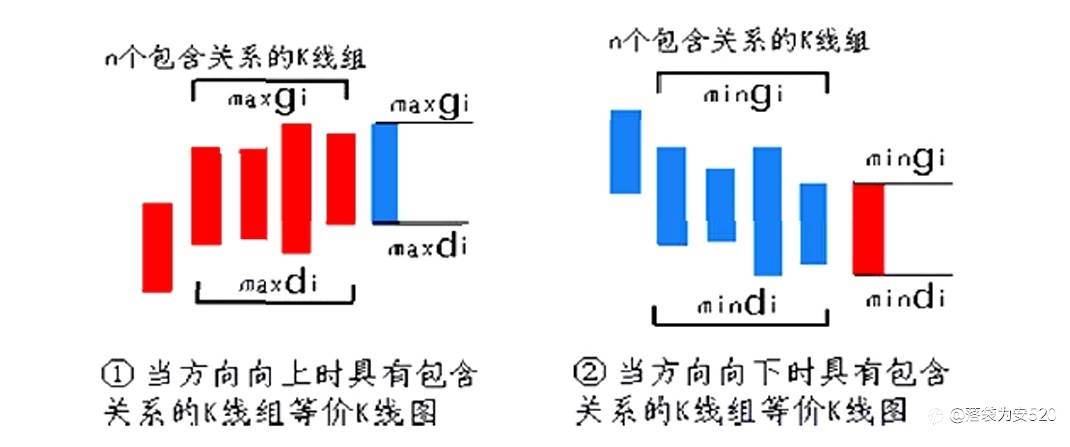
根据上面的方法,用[di,gi]记号第i根K线的最低和最高构成的区间,当向上时,顺次 n 个包含关系的K 线组,等价于[maxdi,maxgi]的区间对应的 K 线,也就是说,这 n个K 线,和最低最高的区间为[maxdi,maxgi]的 K 线是一回事情;向下时,顺次 n 个包含关系的K线组,等价于[mindi,mingi]的区间对应的K线。

已编辑 17 Feb 2021, 15:13
风险提示:以上内容仅代表作者或嘉宾的观点,不代表 FOLLOWME 的任何观点及立场,且不代表 FOLLOWME 同意其说法或描述,也不构成任何投资建议。对于访问者根据 FOLLOWME 社区提供的信息所做出的一切行为,除非另有明确的书面承诺文件,否则本社区不承担任何形式的责任。
FOLLOWME 交易社区网址: followme.asia


加载失败()